
Καποτε ενα μικρο κοριτσι με ανησυχο πνευμα ρωτησε "Γιατι οι σταγονες της βροχης δεν ειναι ποτέ τοσο μεγαλες οσο το κεφαλι μου?" Η φιλη της απαντησε "Κοιτα αν ηταν τοσο μεγαλες θα δυσκολευομασταν να κραταμε την ομπρελα.".
Το ερωτημα ομως παραμενει.
Ισως οι σταγονες της βροχης που πεφτουν απο τα συννεφα ειναι μικρες επειδη δεν εχουν αρκετο χρονο μεσω συσσωματωσης με αλλες, να μεγαλωσουν τοσο πολυ. Αν ομως απο ενα αεροστατο ή ενα ψηλο κτιριο ριξουμε ενα δοχειο νερο ολο μαζι, θα δουμε οτι δεν φτανει ποτέ ως συνολο αυτη η ποσοτητα νερου αλλά φτανει παντοτε με τη μορφη ξεχωριστων σταγονων.
Επομενως κατι καθοριζει το τελικο μεγεθος των σταγονων της βροχης.
Αυτο το κατι ειναι η επιφανειακη ταση. Για να χωρισουμε στη μεση μια σταγονα κατα μηκος του "ισημερινου" της(Σχημα 1) θα χρειαστει να ασκησουμε μια δυναμη Fσ ιση με το γινομενο του μηκους του ισημερινου 2πr και ενος παραγοντα σ που ονομαζεται συντελεστης επιφανειακης τασης.
Ο σ εχει διαστασεις δυναμης προς μηκος και για το νερο ειναι ισος με 0.05 N/m εως 0.08 N/m.
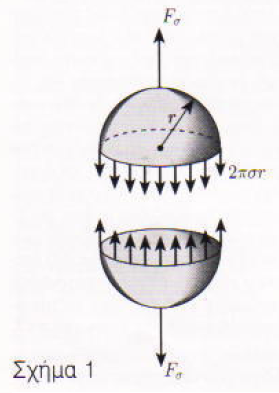
Σκεφτειτε την σαμπρελα μεσα σε μια μπαλα ποδοσφαιρου. Η ταση της σαμπρελας η οποια σε καθε σημειο ειναι εφαπτομενικη στην επιφανεια της, δημιουργει ακτινικες δυναμεις που κατευθυνονται προς το κεντρο της μπαλας και εξισορροπουν την υπερπιεση του αεριου. Στην περιπτωση μιας υγρης σταγονας η επιφανειακη ταση εχει αποτελεσμα μια εσωτερικη υπερπιεση γνωστη ως πιεση Laplace.(Βεβαια η αναλογια αυτη δεν ειναι ακριβης. Η επιφανειακη ταση στην σταγονα και αντιθετα με ο,τι συμβαινει στη μπαλα δεν σχετιζεται πρακτικα με την ακτινα της).
Εξαιτιας αυτων των δυναμεων, μια σταγονα υγρο σε συνθηκες ελλειψης βαρους (πχ σε ενα διαστημικο οχημα σε τροχια) διατηρει σφαιρικο σχημα. Απο την αλλη πλευρα μια σταγονα τοποθετημενη πανω στη στεγνη επιφανεια ενος τραπεζιου αποκτα πεπλατυσμενο σχημα. Πχ μπορει να το δειτε αυτο μετα απο μια βροχη με μια δροσοσταλιδα πανω σε ενα φυλλο.
Με τον ιδιο ακριβως τροπο μια σταγονα βροχης που πεφτει με σταθερη ταχυτητα παιρνει πεπλατυσμενο σχημα λογω της αντιστασης του αερα.
Με λιγα λογια η αντισταση του αερα αλλαζει τη μορφη της σταγονας και η αλλη δυναμη,- η επιφανειακη ταση-, θελει να την επαναφερει στο σφαιρικο σχημα. Επομενως η ισοτητα αυτων των 2 δυναμεων μας παρεχει μια προσεγγιση της ταξης μεγεθους των μεγιστων διαστασεων μιας σταγονας που πεφτει με σταθερη ταχυτητα.
Η ομαλη κινηση λοιπον της σταγονας μας υπαγορευει οτι η δυναμη της αντιστασης του αερα ισουται με το βαρος της. Επομενως:
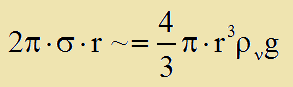
(το ~= σημαινει περιπου ισο, σε ταξη μεγεθους ισο δηληδη)
οπου Ρν η πυκνοτητα του νερου.
Λυνοντας ως προς r εχουμε:
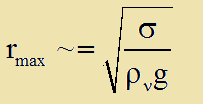
Παραλειψαμε τον ορο ριζα του (6/4) καθως αυτο που ψαχνουμε εδω ειναι μια προσεγγιστικη λυση και την απαντηση στο ερωτημα τι ταξη μεγεθους θα εχουν περιπου οι σταγονες και γιατι δεν γινονται μεγαλες οσο πχ το κεφαλι μας.
Αν αντικαταστησουμε με τα αριθμητικα δεδομενα g = 10 m/s^2 , σ ~= 0.06 N/m , Ρν = 1000 kg/m^3 προκυπτει:
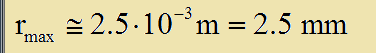
2.5 χιλιοστα δηλαδη περιπου ειναι η μεγιστη ακτινα τους, δηλαδη 5 χιλιοστα ή μισο εκατοστο ειναι περιπου η μεγιστη διαμετρος που μπορουν να αποκτησουν οι σταγονες.
Και πραγματι το συνηθεστερο μεγεθος ειναι περιπου αυτο, χωρις βεβαια να λειπουν και πιο ακραιες περιπτωσεις οπου οι σταγονες ειναι μεγαλυτερες αλλά παντα σε αυτη την ταξη μεγεθους(ακτινα μικροτερη του ενος εκατοστου περιπου).
Βιβλιογραφια:
Περιοδικο QUANTUM Μαιος/Ιουνιος 1994.
Δεν υπάρχουν σχόλια:
Δημοσίευση σχολίου