Οπτικο παραδοξο. Penrose triangles.
Αδυνατο σχημα να κατασκευαστει(ουδεμια σχεση εχει με το παρον θεμα).
Ενα πολυ παλιο αναπαντητο ερωτημα και αλυτο θεμα ηταν οτι δεδομενων 2 τριγωνων, το ενα με πλευρες A,B,C και το αλλο με D,E,F, ποιες συνθηκες(ικανες και καλο θα ηταν να ειναι και αναγκαιες) πρεπει να ισχυουν ωστε το ενα τριγωνο να χωραει μεσα στο αλλο.
Το ερωτημα αυτο εχει εδω και καμια 20αρια χρονια απαντηθει. Η απαντηση δυστυχως δεν ειναι ευρεως γνωστη ενω στην Ελληνικη βιβλιογραφια δεν εχω δει πουθενα να υπαρχει.
Η πρωτη διαισθητικη απαντηση οτι αρκει και οι 3 πλευρες του να ειναι μια προς μια μικροτερες απο τις αλλες, πχ αν A>a, B>b, C>c οπως στο σχημα 1 παρακατω ειναι στην πραγματικοτητα τελειως λαθος. Πχ φαινεται απο το σχημα 1 οτι υπαρχουν περιπτωσεις οπου ακομα και ολες οι πλευρες του να ειναι μικροτερες απο ολες τις πλευρες του αλλου, μπορει να μην χωραει μεσα στο αλλο!
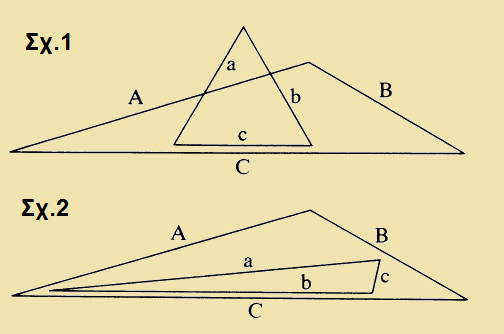
Επισης υπαρχουν περιπτωσεις πχ οπως στο σχημα 2 πανω, οπου παρολο που οι 2 πλευρες του ενος ειναι μεγαλυτερες απο 2 πλευρες του αλλου, πχ a>A, b>B, και ομως το τριγωνο να χωραει!
Η λυση στο προβλημα αυτο ειναι πιο πολυπλοκη απο αυτες τις διαισθητικες προσπαθειες απαντησης.
Πριν δωθει η απαντηση (χωρις αποδειξη) να αναφερω επισης ενα παρομοιο θεμα που εξασφαλιζει την υπαρξη τριγωνου για δεδομενες 3 πλευρες, το οποιο επισης η Ελληνικη βιβλιογραφια αποφευγει να αναφερει, φυσικα δεν αναφερομαι καν για την σχολικη υλη οπου τοσο η υπαρξη του οσο καθως και φυσικα η αποδειξη του λαμπει δια της απουσιας της.
Αναφερομαι φυσικα στην περιφημη τριγωνικη ανισοτητα η οποια ομως συνηθως αναφερεται κατα το ημισυ της. Η ολοκληρωμενη μορφη της ειναι:
Υπαρχει τριγωνο με πλευρες A,B,C αν και μόνο αν A+B>C και A+C>B και B+C>A και A>0, B>0, C>0.
Δηλαδη ισχυουν 2 πραγματα:
1)•Αν υπαρχει τριγωνο με πλευρες A,B,C τοτε ισχυουν: A+B>C και A+C>B και B+C>A και A>0, B>0, C>0.
2)•Αν ισχυουν A+B>C και A+C>B και B+C>A και A>0, B>0, C>0 τοτε ισχυει οτι υπαρχει τριγωνο με πλευρες A,B,C.
Το μεν 1ο ειναι αυτο που αναφερουν ολα τα βιβλια γεωμετριας και μερικα εχοντας και την αποδειξη του, αλλά το 2ο το οποιο ειναι εξισου σημαντικο δεν αναφερεται πουθενα, πόσο μαλλον η αποδειξη του.
Να αναφερω τις αποδειξεις και των 2.
Αποδειξη για το 1):
Εστω εχουμε το τριγωνο ABC.
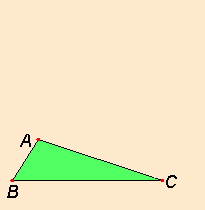
Φερνουμε την προεκταση της BA.
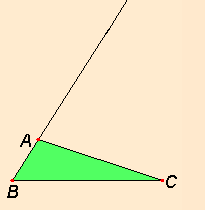
Παιρνουμε σημειο D πανω στην προεκταση αυτη ετσι ωστε AD = AC. (1)
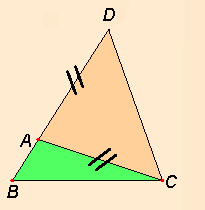
Φυσικα, και συμφωνα με την προταση 5 του 1ου βιβλιου των στοιχειων του Ευκλειδη οι γωνιες ADC και ACD ειναι ισες.
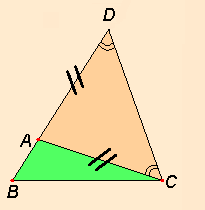
Να σημειωθει εδω οτι μπορουμε να χρησιμοποιησουμε την προαναφερθεισα προταση χωρις πχ να ενδιαφερομαστε ή οχι για το αν ισχυει η τριγωνικη ανισοτητα, δηλαδη αυτο που προσπαθουμε να αποδειξουμε(γιατι πχ σε αντιθετη περιπτωση αν πχ για την αποδειξη της προτασης 5 χρησιμοποιουνταν η τριγωνικη ανισοτητα, τοτε προφανως για να αποδειξουμε την τριγωνικη ανισοτητα δεν θα μπορουσαμε να χρησιμοποιησουμε την προταση 5!), διοτι για την αποδειξη της προτασης 5 δεν χρησιμοποιηθηκε η τριγωνικη ανισοτητα.
Και να αναφερω σε αυτο το σημειο την αξιωματικη θεμελιωση και το χτισιμο πανω σε αυτην με παραγωγικη λογικη, ως προς την παραγωγη ενος ολοκληρωμενου εργου των μαθηματικων(που χρησιμοποιειται ακομα και σημερα, 2300 χρονια μετα!), που εφερε ο Ευκλειδης για πρωτη φορα στα χρονικα της ιστοριας!! Αρχικα εθεσε καποια αξιωματα ως αληθη και μετα τα χρησιμοποιησε για να αποδεικνυει καθε φορα καποια θεωρηματα, και πανω σε αυτα νεα θεωρηματα κλπ. Οποτε παιζει ρόλο η σειρα με την οποια παρηχθησαν τα θεωρηματα.
Το παραπανω εχει νοημα που θα αναδειχτει παρακατω.
Εχουμε λοιπον το σχημα:

Και ειπαμε οτι οι γωνιες ADC και ACD ειναι ισες.
Επισης ειναι φανερο οτι η γωνια BCD > ACD αρα και γωνια BCD > ADC.
Αρα στο τριγωνο BCD η γωνια BCD ειναι μεγαλυτερη απο την ADC.
Και συμφωνα με την προταση 19 του 1ου βιβλιου των στοιχεων του Ευκλειδη, και οι πλευρα απεναντι απο την μεγαλυτερη γωνια θα ειναι μεγαλυτερη.
Αρα BD > BC.
Και εδω πρεπει να σημειωθει οτι η προταση 19 μπορει να χρησιμοποιηθει για ακριβως αυτο τον λογο. Οτι για να αποδειχτει δεν χρειαστηκε η τριγωνικη ανισοτητα.
Η οποια τριγωνικη ανισοτητα που αποδεικνυουμε εδω, ειναι βασικα η προταση 20 του 1ου βιβλιου στοιχειων του Ευκλειδη. Οποτε μπορουμε να χρησιμοποιησουμε για να την δειξουμε ολες τις προηγουμενες προτασεις απο 1 εως 19 του 1ου βιβλιου, καθως και τα θεμελιωδη αξιωματα βεβαια(αξιωματα οπως τα λεμε τωρα γιατι ο Ευκλειδης τα χωριζε σε αξιωματα και αιτηματα αλλά η ουσιαστικη διαφορά τους δεν εχει κανενα νοημα).
Ετσι λοιπον ειπαμε οτι ισχυει BD > BC.
Ομως BD = BA + AD αρα ισχυει ΒΑ + AD > ΒC.
Αρα λογω (1) θα ισχυει τελικως: ΒΑ + AC > ΒC.
ο.ε.δ.
**Το ο.ε.δ. προερχεται απο το οπερ εδει δειξαι, το οποιο σημαινει "αυτο ακριβως που επρεπε να αποδειξουμε" δηλαδη δηλωνει οτι η αποδειξη ολοκληρωθηκε και ειναι αυτη που επρεπε να ειναι.
Με τον ιδιο και αντιστοιχο τροπο βεβαια δειχνουμε και οτι ΒΑ + BC > AC και ΒC + AC > ΑΒ.
Αρα αποδειχτηκε η 1).
Αποδειξη για το 2):
Εστω 3 πραγματικοι αριθμοι A,B,C ετσι ωστε: A+B>C και A+C>B και B+C>A και A>0, B>0, C>0.
Παιρνουμε τα 3 σημεια του επιπεδου:
(0,0) , (Α,0) , (x,y)
Με x,y που δινονται απο:
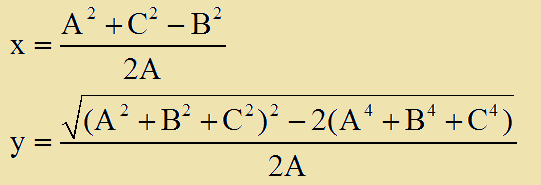
Το x ειναι πραγματικος αριθμος.
Εαν τωρα ισχυει οτι και ο y ειναι πραγματικος αριθμος και μεγαλυτερος του μηδενος, τοτε, και επειδη:
d|(0,0),(A,0)| = A
d|(0,0),(x,y)| = C
d|(A,0),(x,y)| = B
........ειναι φανερο(αφου οι γωνιες των 2 ευθυγραμμων τμηματων που οριζονται απο τα (0,0) και (x,y) καθως και (Α,0) και (x,y), με τον αξονα των τετμημενων(y=0) θα ειναι διαφορες του μηδενος--αφου y>0) οτι θα οριζεται τριγωνο ABC.
**To d|(α,β),(γ,δ)| δινει την αποσταση μεταξυ των σημειων (α,β) και (γ,δ) του επιπεδου.
Οποτε αυτο που πρεπει να αποδειξουμε ειναι οτι y ειναι πραγματικος αριθμος και y>0.
Αρκει δηλαδη να δειξουμε οτι
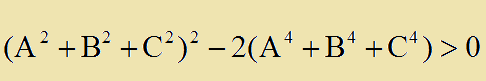
Ουσιαστικα δηλαδη θελουμε να δειξουμε οτι η επομενη συνεπαγωγη ειναι αληθης:
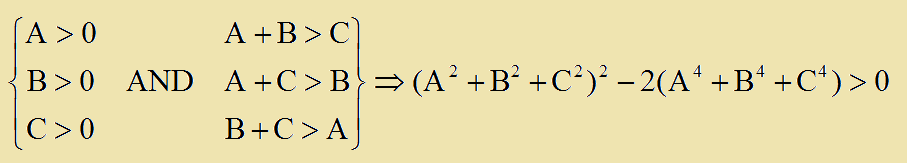
Αποδειξη:
Ισχυουν οι ισοδυναμιες:
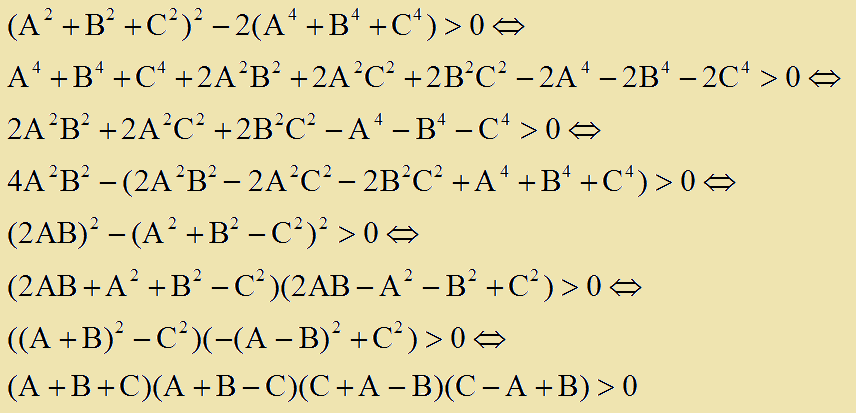
Και λογω υποθεσης η τελευταια σχεση ειναι φανερο οτι ισχυει αρα ισχυει και:
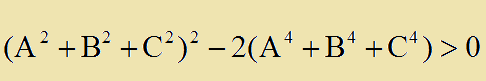
Αρα y ειναι πραγματικος αριθμος και μαλιστα μεγαλυτερος του μηδεν, αρα υπαρχει τριγωνο με πλευρες A,B,C.
ο.ε.δ.
Αρα καθε φορα που εχουμε 3 ευθυγραμμα τμηματα A,B,C, εαν ισχυουν και οι 3 σχεσεις A+B>C, A+C>B, B+C>A τοτε μπορει να σχηματιστει τριγωνο με πλευρες αυτα τα ευθυγραμμα τμηματα. Αυτες οι 3 ανισοτητες δηλαδη αποτελουν δηλαδη ικανη συνθηκη για να υπαρξει τριγωνο.
Απο την αλλη και λογω του 1) αποτελουν και αναγκαια συνθηκη. Δηλαδη δεν υπαρχει τριγωνο οπου αυτες οι 3 ανισοτητες να μην ισχυουν.
Penrose triangles.
Ξαναπηγαινοντας λοιπον πισω στο αρχικο θεμα του αν χωραει ενα τριγωνο μεσα σε καποιο αλλο και ποιες ειναι οι αναγκαιες και ικανες συνθηκες για κατι τετοιο, τοτε αποδεικνυεται οτι:
►Εαν εχουμε ενα τριγωνο με πλευρες A,B,C και ενα αλλο με πλευρες D,E,F τοτε ικανη και αναγκαια συνθηκη για να χωραει το τριγωνο DEF μεσα στο ABC, ειναι να ισχυει μια ή και περισσοτερες απο τις παρακατω 18 ανισοτητες:
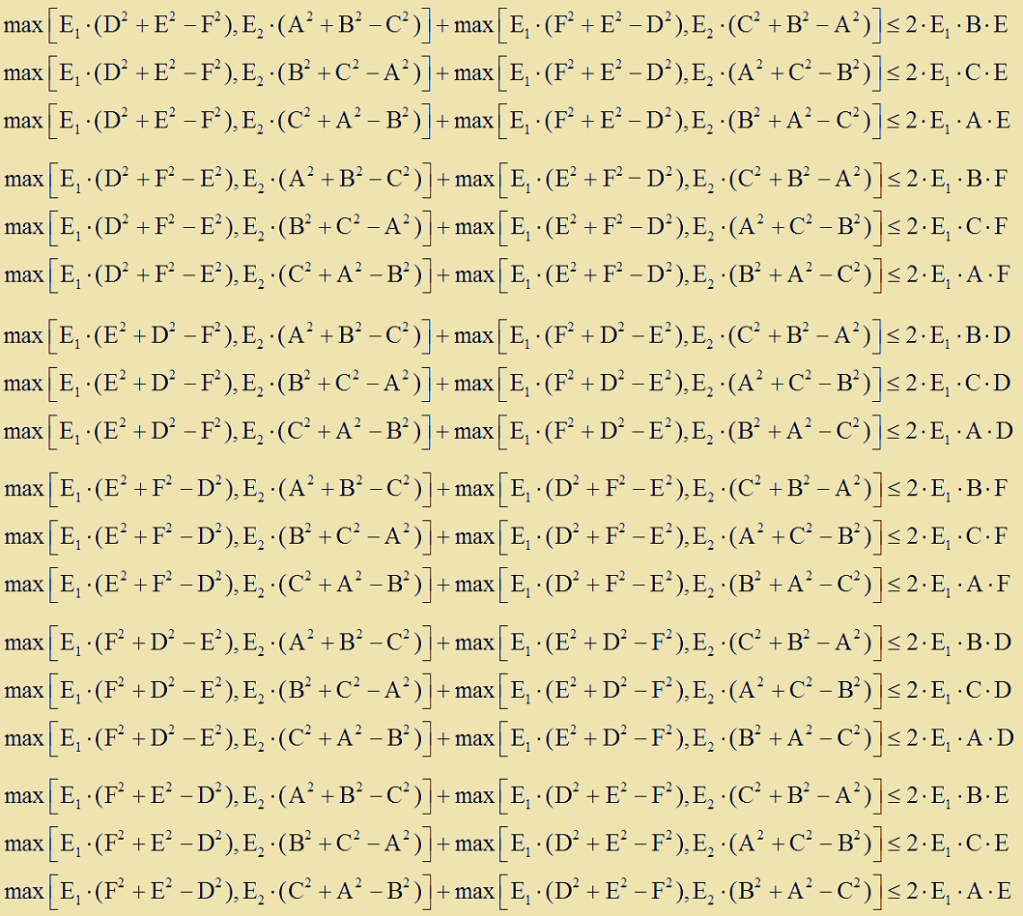
οπου:
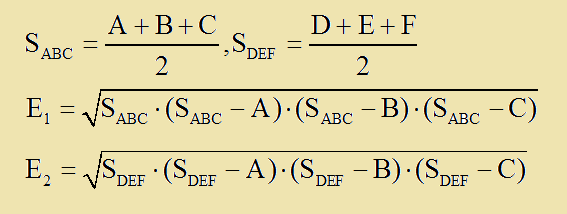
Αυτες οι 18 ανισοτητες φαινονται πολλες αλλά στην ουσια μπορουν ευκολα να συρρικνωθουν σε μια απο την οποια μπορουν να προκυψουν οι αλλες 17.
Η μια εξισωση ειναι η:
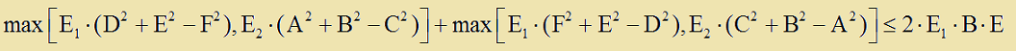
Και απο την οποια με αντικατασταση των {A,B,C} και {D,E,F} με καποιον απο τους εξης συνδιασμους:
Για το {A,B,C}: (3 συνδιασμοι)
{A,B,C}
{B,C,Α}
{C,A,B}
Για το {D,E,F}: (6 συνδιασμοι)
{D,E,F}
{D,F,E}
{E,D,F}
{E,F,D}
{F,D,E}
{F,E,D}
Oπότε παιρνοντας(διαλεγοντας) ενα συνδιασμο για το {A,B,C} και ενα για το {D,E,F} και αλλαζοντας καταλληλα τις μεταβλητες στην εξιωση μπορουν να "γεννηθουν" 3·6 = 18 συνδιασμοι.
Η εξισωση αυτη μας λεει(ικανη συνθηκη) οτι αν για τις 6 πλευρες 2 τριγωνων ισχυει εστω και μόνο μια απο τις ανισοτητες αυτες, τοτε το ενα τριγωνο χωραει μεσα στο αλλο. Αν ισχυουν φυσικα παραπανω απο μια ανισοτητες, καμια ουσιαστικη διαφορα δεν εχει.
Επισης μας λεει(αναγκαια συνθηκη) οτι ειναι αδυνατον να υπαρχουν περιπτωσεις τριγωνων που να χωρουν το ενα μεσα στο αλλο και να μην υπαρχει εστω και μια απο αυτες τις 18 ανισοτητες που να μην ειναι αληθης.
Δηλαδη οι 18 αυτες εξισωσεις μας δινουν την δυνατοτητα να γνωριζουμε τα παντα σχετικα με το πότε ενα τριγωνο χωραει μεσα σε ενα αλλο.
Μερικα παραδειγματα:
•Το τριγωνο με πλευρες 3,5,5(και υπαρχει τριγωνο με αυτες τις πλευρες-καθως αν θυμηθουμε και απο τα προηγουμενα περι τριγωνικης ανισοτητας- ισχυουν και 3+5>5 και 5+5>3) δεν χωραει μεσα στο τριγωνο με πλευρες 4,5,7(και υπαρχει τριγωνο με αυτες τις πλευρες καθως ισχυουν και 4+5>7 και 4+7>5 και 5+7>4) καθως και οι 18 ανισοτητες δεν ισχυουν.
•Το τριγωνο ομως με πλευρες 3,5,6(και υπαρχει τριγωνο με αυτες τις πλευρες καθως ισχυουν και 3+5>6 και 3+6>5 και 6+5>3) χωραει μεσα στο τριγωνο με πλευρες 4,5,7 καθως οι ανισοτητες 1 και 11 απο τις παραπανω 18 ισχυουν!
Δηλαδη μεσα στο τριγωνο με πλευρες {4,5,7}, το τριγωνο {3,5,5} ΔΕΝ χωραει, ενω το τριγωνο {3,5,6} χωραει!!
Δηλαδη το τριγωνο {3,5,5} ενω δεν χωραει μεσα στο {4,5,7}, αν του αυξησουμε μια πλευρα κατα μια μοναδα μηκους τοτε αυτο θα χωραει!!
Εχουμε δηλαδη κατι που δυσκολα το περιμενουμε διαισθητικα.
•Το τριγωνο με πλευρες 4,4,4(και υπαρχει τριγωνο με αυτες τις πλευρες καθως 4+4>4) δεν χωραει μεσα στο τριγωνο με πλευρες 5,8,11(και υπαρχει τριγωνο με αυτες τις πλευρες καθως ισχυουν τα 5+8>11 και 5+11>8 και 11+8>5) καθως και οι 18 ανισοτητες δεν ισχυουν.
•Το τριγωνο με πλευρες 5,6,7(και υπαρχει τριγωνο με αυτες τις πλευρες καθως ισχυουν 5+6>7 και 5+7>6 και 6+7>5) χωραει μεσα στο τριγωνο με πλευρες 5,8,9(και υπαρχει τριγωνο με αυτες τις πλευρες καθως ισχυουν τα 5+8>9 και 5+9>8 και 9+8>5) καθως ισχυει η ανισοτητα 18. Και μόνο αυτη ισχυει ενω οι αλλες 17 δεν ισχυουν αλλά οπως ειπαμε ειναι αρκετη ωστε να κανει το τριγωνο να χωραει μεσα στο αλλο!
•Το τριγωνο με πλευρες 7.1,7.9,8.8(και υπαρχει τριγωνο με αυτες τις πλευρες καθως ισχυουν 7.1+7.9>8.8 και 7.1+8.8>7.9 και 7.9+8.8>7.1) χωραει μεσα στο τριγωνο με πλευρες 8,9,9(και υπαρχει τριγωνο με αυτες τις πλευρες καθως ισχυουν τα 9+8>9 και 9+9>8) καθως ισχυει η ανισοτητα 2 και η 18.
Δεν υπάρχουν σχόλια:
Δημοσίευση σχολίου