Διαβαζοντας ενα πολυ καλο καιρικο μπλογκ ενος πολυ λογικου ανθρωπου(συνηθιζω να χωριζω τους ανθρωπους σε λογικους επιστημονες, σε λογικους μη επιστημονες, σε "αδιαφορους" και σε μη λογικους) που ουτε καν τον ξερω προσωπικα, απλως διαβαζω τις αποψεις του μεσα σε ενα καιρικο φορουμ που γραφει(hellasweather.gr) καθως και απο το καιρικο μπλογκ του(παροτι τωρα αρχισα να το διαβαζω) και διαπιστωσα, μερικα μικρολαθακια κακων/ελλειπων διατυπωσεων που μπορουν να παρερμηνευτουν, σε ενα θεμα.
Σε τουτο:
http://antisimvatikos.blogspot.gr/2011/08/blog-post.html
Ετσι λοιπον εχουμε οτι αναφερει:
"Ας ξεκινήσουμε από τον απλό υπολογισμό του πόσο μακριά είναι ο ορίζοντας (η νοητή γραμμή στην οποία θάλασσα και ουρανός γίνονται ένα), δηλαδή πόσο μακριά μπορούμε να δούμε σε μια καθαρή μέρα."
Αυτη η προταση, αν και ο δημιουργος της μαλλον εννοουσε πόσο μακρυα μπορουμε να δουμε ενα αντικειμενο που βρισκεται στην επιφανεια της γης, μπορει να παραπλανησει, καθως η αποσταση που μπορει να δουμε σε μια καθαρη μερα ειναι πολλα τρισεκατομμυρια χιλιομετρα μακρυα! Πχ τα αστερια που βλεπουμε στον ουρανο βρισκονται ακομα και πανω απο 150 τρισεκατομμυρια χιλιομετρα μακρυα μας. Και ομως μπορουμε να τα δουμε! Μπορουμε να δουμε δηλαδη σε αποσταση 150 τρισεκατομμυριων χιλιομετρων μακρυα μας!!
Εαν εννοουσε πόσο μακρυα μπορουμε να δουμε ενα (σημειακο) αντικειμενο στην επιφανειας της γης, τοτε ναι οι υπολογισμοι του ειναι σωστοι φυσικα, αν και στην πραγματικοτητα υπαρχουν και φαινομενα ατμοσφαιρικης διαθλασης/σκεδασης κλπ, ωστε το φως να καμπτεται και ετσι να μπορουμε να δουμε λιγο παραπανω πισω απο τον οριζοντα μας απο οτι με τους παραπανω υπολογισμους(μια πολυ καλη προσεγγιστικη σχεση με εξαιρετικα αποτελεσματα ειναι θετοντας την ακτινα της γης ισης με τα 7/6 της πραγματικης-θεωρωντας την γη ως σφαιρα με ακτινα 6378 km).
Επειτα παμε παρακατω στο εξης που αναφερει:
"Ένας γενικός τύπος που υπολογίζει τις αποστάσεις στις οποίες μπορούμε να δούμε όταν εμείς είμαστε σε ύψος h_1 και το αντικείμενο έχει ύψος h_2, ακολουθεί στην επόμενη εικόνα."
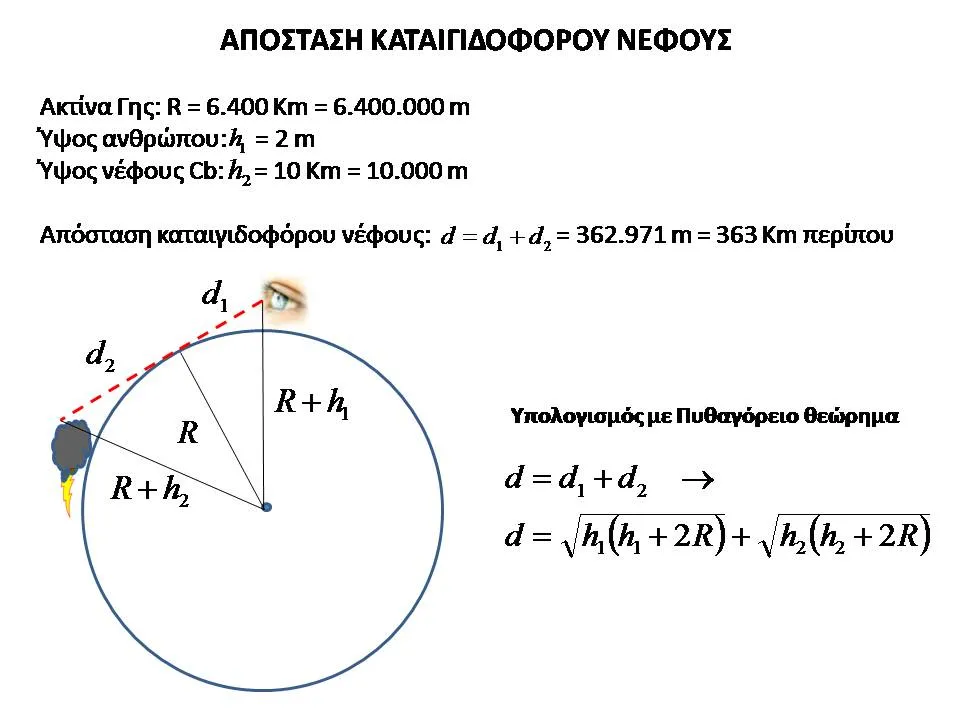
"Εδώ φαίνεται πως ένα καταιγιδοφόρο νέφος που φτάνει σε ύψος, χοντρικά, τα 10 Km, είναι ορατό από απόσταση 360 Km περίπου. "
Η παραπανω ηταν μια αλλη παραπλανητικη προταση που μπορει επισης να οδηγησει σε μεγαλες παρερμηνευσεις. Το μόνο που χρειαζεται βασικα για να γινει σωστη ειναι να προστεθει η λεξη "μεγιστο" σε αυτην.
Ο παραπανω τυπος δηλαδη υπολογιζει την μεγιστη αποσταση που μπορει να δει καποιος ενα αντικειμενο με υψος h2 και οχι την αποσταση που μπορει να δει καποιος ενα αντικειμενο με υψος h2(ασαφης προταση).
Εφοσον δε, παρουμε ως υψος cumulonimbus νεφους το μεγιστο υψος που μπορει να φτασει(μιας και θεωρητικα δεν υπαρχει καποιο σαφες ιδιαιτερο οριο(παροτι φυσικα η εξωσφαιρα αποτελει σιγουρο ανωτατο οριο αλλά μιλαμε για ρεαλιστικο ανωτατο οριο) αλλά μπορουμε να παρουμε το ρεκορ μεγιστου υψους για νεφος cumulonimbus που ειναι 23 χιλιομετρα), βρισκουμε και την μεγιστη αποσταση που μπορει να δει κανείς ενα συννεφο cumulonimbus.
Ας δουμε τωρα γιατι ειναι η μεγιστη αποσταση που μπορουμε να δουμε ειναι αυτη. Ας την ονομασουμε hmax. Στην περιπτωση μας ισχυει hmax = 23 km αλλά το hmax μπορει να παρει οποιαδηποτε τιμη ωστε να βρουμε την μεγιστη αποσταση που μπορουμε να δουμε ενα αντικειμενο με υψος hmax.
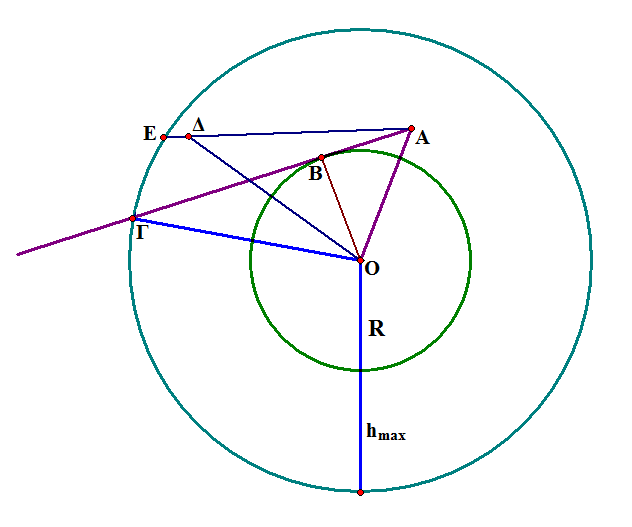
Εχουμε αρχικα οτι μιλαμε για σφαιρικη γη και οτι εμεις(τα ματια μας) βρισκομαστε στο Α, σε υψος δηλαδη απο την επιφανεια της γης h = (ΟΑ) - R, οπου R η ακτινα της γης.
Παιρνουμε επισης μια ημιευθεια Αx και ενα ευθυγραμμο τμημα ΑΓ που περνα απο τον οριζοντα μας και τεμνει την επιφανεια της γης στο Β. Δηλαδη εχουμε το σχημα:
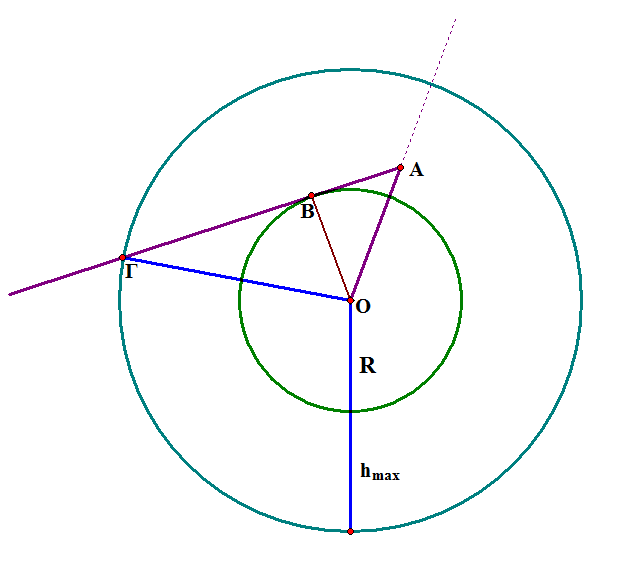
Το ορατο πεδιο μας ειναι αυτο που ειναι πανω απο τον οριζοντα ή ακριβως σε αυτον. Παροτι οπως αναφεραμε προηγουμενως λογω φαινομενων ατμοσφαιρικης διαθλασης/σκεδασης κλπ, που κανουν το φως να καμπτεται, μπορουμε να δουμε λιγο παραπανω πισω απο τον οριζοντα μας οποτε το οπτικο πεδιο μας ειναι λιγο μεγαλυτερο.
Αλλά τελοσπαντων το ορατο πεδιο μας ειναι αυτο που ειναι σημειωμενο με κιτρινο. Βεβαια, παιρνουμε μόνο την μια εκ των 2 συμμετρικων περιπτωσεων, δηλαδη το πορτοκαλι γραμμοσκιασμενο τμημα "δεξιοτερα" του ευθυγραμμου τμηματος που περνα απο εμας και το κεντρο της γης, καθως η αντιμετωπιση που μπορουμε να εχουμε για αυτο το τμημα ειναι παντελως ομοια με αυτην που θα εχουμε παρακατω για το "αριστερο" τμημα.
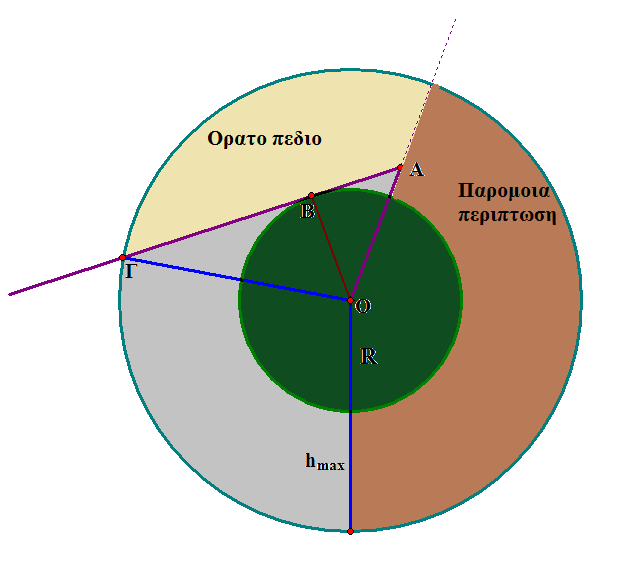
Για να δειξουμε οτι το σημειο Γ οριζει την μεγιστη αποσταση(AΓ) που μπορουμε να δουμε ενα συννεφο cumulonimbus, παιρνουμε ενα τυχαιο σημειο μεσα απο το δυνατο ορατο μας πεδιο, εστω Δ.
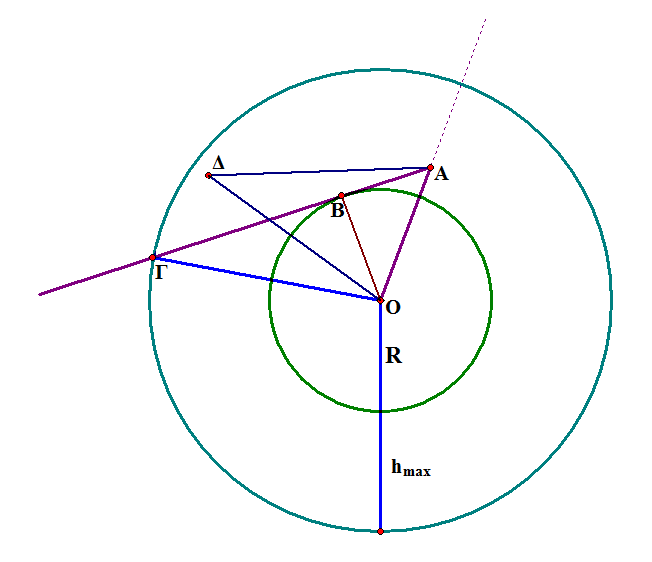
Προεκτεινουμε το ευθυγραμμο τμημα ΑΔ και ονομαζουμε Ε το σημειο τομης της προεκτασης του με τον κυκλο με κεντρο το κεντρο της γης και ακτινα ιση με hmax, στο τμημα του ορατου πεδιου παντα.
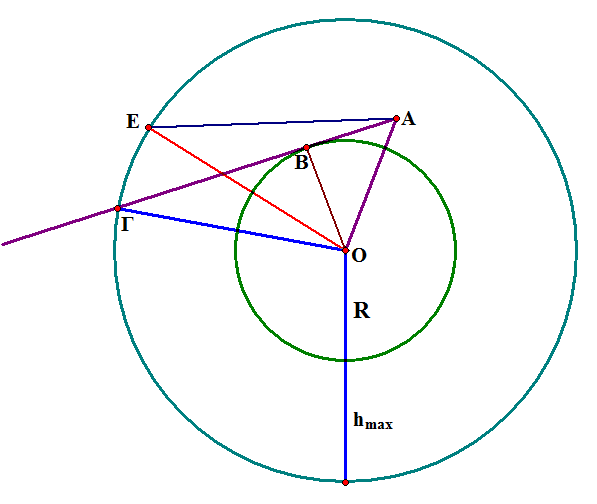
Προφανως ΑΕ > ΑΔ αρα πρεπει να δειξουμε οτι ΑΓ >ΑΕ :
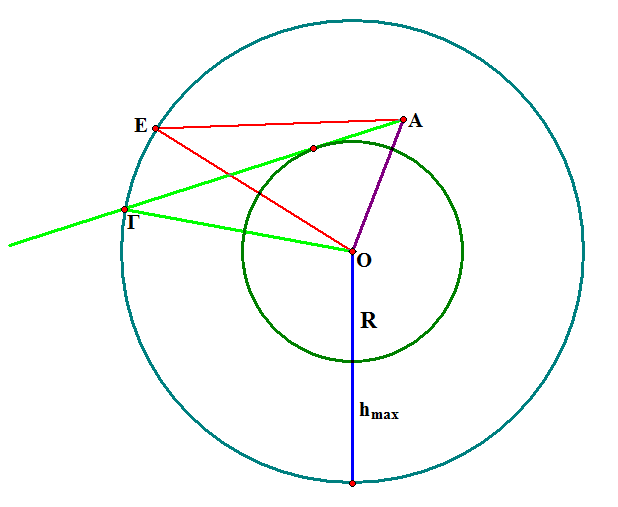
Αυτο ειναι αμεσα σαφες οτι ισχυει καθως τα τριγωνα ΟΑΕ και ΟΑΓ εχουν κοινη την ΑΟ, αντιστοιχα ισες πλευρες τις ΕΟ και ΓΟ, ενω οι αντιστοιχες περιοχομενες σε αυτες γωνιες ειναι οι ΑΟΕ και ΑΟΓ. Ομως ισχυει γωνια ΑΟΕ < γωνια ΑΟΓ οποτε λογω του σχετικα γνωστου βασικου θεωρηματος που δεν χρειαζεται να αποδειξουμε εδω, επεται οτι και η πλευρα απεναντι απο την μεγαλυτερη γωνια θα ειναι μεγαλυτερη.
Απο το παρακατω σχημα που δειχνει 2 ιδιου υψους νεφη cumulonimbus με κορυφες στα Δ και Ε, φαινεται οτι οι αποστασεις τους απο εμας μπορει να ειναι διαφορετικες, αρα αυτο σημαινει οτι δεν υπαρχει μονοσημαντη αντιστοιχια αποστασης της κορυφης του υψους απο εμας, με το υψος του.
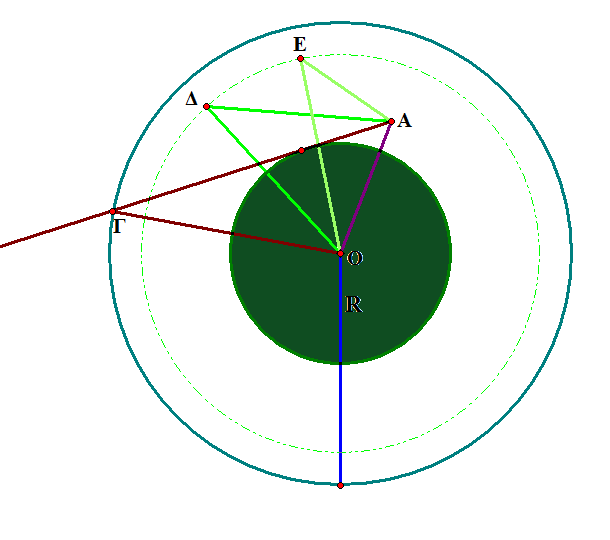
Υπολογιζοντας επισης την μεγιστη αποσταση οπου μπορουμε να δουμε ενα νεφος cumulonimbus, θετουμε hmax = 23 km και απο τον τυπο που αναφερθηκε προηγουμενως και τον ξαναγραφουμε εδω:
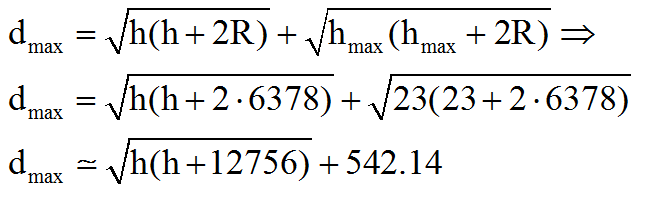
Εδω να σταθουμε μια στιγμη και να γραψουμε την σωστη αναπαρασταση της εξισωσης, διοτι η παραπανω(ολες οι παραπανω βασικα) ειναι λανθασμενη αλλά χρησιμοποιειται ευρεως για λογους απλοτητας. Η σωστη λοιπον γραφη ειναι:
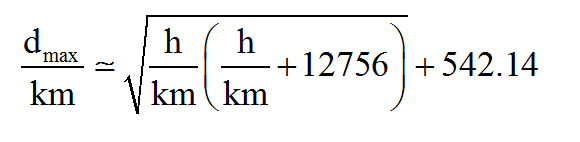
Η γραφη h/km πχ χρησιμοποιειται γιατι η μεταβλητη h ειναι μια φυσικη ποσοτητα που αναπαριστα και αντιστοιχει σε ποσοτητα αποστασης(του υψους), πχ h = 67 μετρα ή h = 12 km, ή h = 7000 εκατοστα κλπ. Οποτε θετοντας πχ h = 67 m στην εκφραση h/km εχουμε 67 m / km = 67/1000 = 0.067 που ειναι μια αριθμητικη τιμη και αρα εχει νοημα η εξισωση μας.
Ενω τελικως στο δεξιο μερος θα προκυψει ενας αριθμος(μια αριθμητικη τιμη) ενω στο αριστερο θα εχουμε την αριθμητικη τιμη dmax/km.
Δηλαδη πχ θα εχουμε dmax/km = 380 , αρα συνεπαγεται dmax = 380 km.
Ετσι λοιπον βλεπουμε οτι η μεγιστη αποσταση που μπορουμε να δουμε εξαρταται απο το υψος h που βρισκομαστε, οποτε για διάφορα υψη που βρισκομαστε μπορουμε να βρουμε μεσω του παραπανω τυπου την μεγιστη αποσταση που μπορουμε να δουμε ενα συννεφο cumulonimbus, αρα για:
•h = 2 μετρα, δηλαδη στην επιφανεια της θαλασσας και στεκομενοι ορθιοι: d ~= 547 km
•h = 100 μετρα : d ~= 578 km
•h = 1000 μετρα : d ~= 655 km
•h = 8848 μετρα : d ~= 878 km
Ας δουμε τωρα πως μπορουμε να βρουμε την αποσταση απο εμας απο το σημειο οπου εγινε η ηλεκτρικη εκκενωση που προκαλεσε εναν κεραυνο. Η συνηθης και που πρακτικη τακτικη ειναι να μετραμε πόσα δευτερολεπτα χρειαστηκε ο ηχος να φτασει σε εμας απο τη στιγμη που βλεπουμε το φως(που ειναι πρακτικα ιση με την στιγμη της "παραγωγης" του ηχου και της εκκινησης του προς ολες τις κατευθυνσεις και προς τα εμας) και να τα πολλαπλασιαζουμε με το 340(θεωρωντας ως σταθερη ταχυτητα του ηχου σοτν αερα ιση με 340 m/s) και το αποτελεσμα να εισαι σε μετρα. Πχ αν χρειαστηκε 10 δευτερολεπτα να ερθει ο ηχος απο τη στιγμη που ειδαμε την αστραπη, τοτε λεμε οτι η εκκενωση απεχει 3400 μετρα ή 3.5 χιλιομετρα περιπου.
Ομως η διαδικασια αυτη παροτι φοβερα πρακτικη και σχετικα καλης ακριβειας στην πραγματικοτητα εχει σχετικα σαθρο υποβαθρο καθως η ταχυτητα του ηχου στον αερα εξαρταται απο την θερμοκρασια(και μόνο απο αυτην και οχι πχ απο την ατμοσφαιρικη πιεση, σε ενα βουνο πχ με μια θερμοκρασια 20 °C και πιεση 950 hPa, ο ηχος θα ταξιδευει με την ιδια ταχυτητα με οση θα ταξιδευε στην επιφανεια της θαλασσας με πιεση πχ 1010 mbar(hPa) και θερμοκρασια παλι 20 °C) και στα 10 περιπου χιλιομετρα που αναπτυσσονται τα περισσοτερα cumulonimbus η θερμοκρασια καθε αλλο παρα ειναι κοντα στις θετικες τιμες της κλιμακας Κελσιου και μαλιστα στην θερμοκρασια των 15 °C που υπονοει/αντιστοιχει η τιμη των 340 m/s που χρησιμοποιουμε στον πρακτικο τυπο.
Ας παμε λοιπον να δουμε μια πολυ πιο ακριβη(οχι και παλι την ακριβεστερη) προσεγγιση του θεματος.
Εχουμε ενα σημειο Β λοιπον οπου γινεται η ηλεκτρικη εκκενωση. Στο σημειο Α βρισκομαστε εμεις, ενω θελουμε να βρουμε την αποσταση d που ειναι η αποσταση που ταξιδεψε ο ηχος για να ερθει σε εμας.
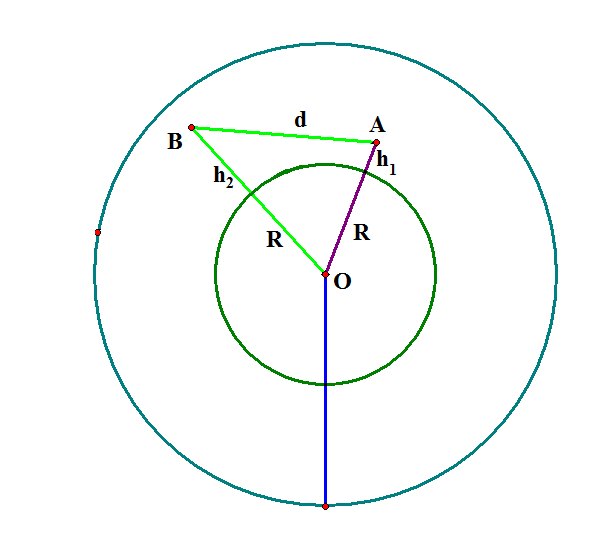
Με την πολυ ορθη υποθεση οτι η μεση θερμοκρασια Τ, που διενυσε ο ηχος μεταξυ του σημειου Β και του σημειου Α(εκει που ειμαστε εμεις), ειναι κατα πολυ καλη προσεγγιση ιδια με αυτην που θα διενυσε εαν εκανε την διαδρομη Β προς το σημειο Γ πανω στην ΟΒ που απεχει απο την επιφανεια της γης αποσταση h1 ιση με το υψος που βρισκομαστε δηλαδη, με αυτη την υποθεση λοιπον εχουμε τα εξης:
Χρησιμοποιωντας την υψομετρικη εξισωση λυνουμε ως προς την θερμοκρασια(βλεπε παρακατω).
Οποτε εχουμε αγνωστο το υψος του συννεφου h2.
Επισης απο την εξισωση d = Sair·t οπου t ο χρονος που μετραμε οπως και πριν(απο τη στιγμη που βλεπουμε την αστραπη εως οτους ακουμε την βροντη της) και Sair η μεση ταχυτητα του ηχου καθολη την διαδρομη, θελουμε να βρουμε την αποσταση μας d απο το συννεφο.
Επισης η ταχυτητα του ηχου εξαρταται απο την μεση θερμοκρασια με τον τροπο που βλεπουμε παρακατω.

Οπως βλεπουμε εχουμε 4 αγνωστους(T,h2,d,Sair) και 3 εξισωσεις αρα πρεπει να αποφασισουμε τι θελουμε να βρουμε.
Εστω οτι θελουμε να βρουμε την αποσταση d οπως ειπαμε και παραπανω.
Τοτε πρεπει να βρουμε ειτε την μεση θερμοκρασια μεταξυ Β και Α, ή μεταξυ Β και Γ διαδρομης, ή την μεση ταχυτητα που θα εχει ο ηχος καθολη την διαδρομη ειτε το υψος του συννεφου.
Αν πχ το υψος ειναι h2 = 10 km, ενω ξερουμε οτι η πιεση στα 10 χιλιομετρα ειναι περιπου P2 = 250 hPa, ενω αν βρισκομαστε σε υψομετρο πχ h1= 100 μετρα, με πιεση P1 = 1010 hPa, και σε γεωγραφικο πλατος 40.65° βορεια, αρα υπολογιζοντας την επιταχυνση της βαρυτητας ιση με g = 9.80228 m/s2, και εαν εκανε ο ηχος 10 δευτερολεπτα να φτασει, τοτε βρισκουμε οτι:
μεση Τ ~= -28.6 °C
Sair~= 313.5 m/s και αρα και:
d = 10·313.5 = 3135 μετρα.
Να θυμηθουμε οτι η πρακτικη μεθοδος εδωσε 3400 μετρα δηλαδη 265 μετρα παραπανω.
Μπορει να μην εχει καμια σχεδον πρακτικη αξια ο παραπανω τροπος να βρισκουμε την αποσταση απο ενα συννεφο αλλά η αντιμετωπιση ειναι που μετραει και που ειναι η ορθη καθως η πρακτικη μεθοδος υποθετει σταθερη ταχυτητα του ηχου απο τα 5-7-8-9 ή τελοσπαντων σε οσα χιλιομετρα γινεται η ηλεκτρικη εκκενωση, εως και τον παρατηρητη, και αρα υποθετει σταθερη θερμοκρασια απο τα 5-10 χιλιομετρα εως και το εδαφος, κατι που δεν θα μπορουσε να ειναι πιο αναληθες.
Και ομως οπως βλεπουμε απο τα τελικα αποτελεσματα, μπορει η πρακτικη μεθοδος να ηταν 265 μετρα μακρια απο την ορθοτερη προσεγγιση, αλλά εχουν αραγε καμια μεγαλη σημασια αυτα τα 265 μετρα που επεσε εξω η πρακτικη μεθοδος? Ειναι σαφες και εκπληκτικο συναμα, οτι με την πρακτικη μεθοδο με ενα πολλαπλασιασμο και μόνο ειχαμε σε τουτο το παραδειγμα σφαλμα μόνο 8.5% περιπου!! Εντυπωσιακο θα ελεγα, αν και η πολυ ορθοτερη θεωρηση του θεματος παραμενει ορθοτερη θεωρηση εστω και πρακτικα δυσχρηστη εως και αχρηστη. :)
Ωραίο το άρθρο φίλε bobby. Αν και διαρρηγνύεις ανοιχτές θύρες, όπως σχολίασα και στο άρθρο μου, καθώς προφανώς και πρόκειται για χοντρική προσέγγιση (αναγράφεται πάνω πάνω) που απαντά σε απορίες της στιγμής. Γράφτηκε εντός 5' και αν η τόσο ασαφής, χοντρική, παραπλανητική, λανθασμένη και πρόχειρη προσέγγιση μου έπεσε μόλις 8.5% έξω σύμφωνα με το δικό σου σχόλιο, τότε δεν πήγε και άσχημα. Θα μπορούσες να πεις (και αυτό είναι το πιο σωστό και καλοπροαίρετο) ότι "αυτή είναι μία χοντρική προσέγγιση... και παρακάτω θα σας παρουσιάσω, με βάση αυτή, μία αναλυτικότερη δική μου προσέγγιση κ.λπ." χωρίς όλους τους χαρακτηρισμούς που είναι άστοχοι σε εξαρχής δηλωμένο ως "χοντρική προσέγγιση" άρθρο γραμμένο σε 5' για να εξηγήσει απορίες της στιγμής.
ΑπάντησηΔιαγραφήΤζαμπα εξαπτεσαι. Οι προθεσεις μου ειναι παντα και ηταν και εδω καλοπροαιρετες. :)
ΑπάντησηΔιαγραφήΕπισης οι εκφρασεις/χαρακτηρισμοι μου, που αναφερεις, δεν αφορουσαν και δεν αναφερονταν στο προσεγγιστικο του θεματος αλλά σε κατι αλλο. Στα συγκεκριμενα πραγματα που ανεφερα και παραπανω(στο οτι δεν εβαλες την λεξη μεγιστο στην 2η περιπτωση και οτι δεν ανεφερες το οτι μιλαμε για αντικειμενα πανω στην επιφανεια της γης) και δεν εχουν να κανουν με το οτι η προσεγγιση σου ηταν "χοντρικη" κλπ.
Οι χαρακτηρισμοι παραπλανητικη, ασαφης, λανθασμενη, κλπ, μπορει να μοιαζουν προσβλητικοι αλλά δεν ειναι! Δεν ηταν αυτος ο σκοπος μου φυσικα, παροτι ισως μοιαζει ετσι και προφανως ετσι τον εξελαβες....
Για μικρές αποστάσεις, η καμπυλότητα της γης δε λαμβάνεται υπ' όψιν νομίζω καθόλου. Φιλικά Γιώργος.
ΑπάντησηΔιαγραφή