Η θερμοκρασια αυτη ειναι ιδιαιτερως σημαντικη και παρολο τον ολιγον φαινομενικα ανουσιας σημασιας ορισμο, εχει ιδιαιτερη σημασια στα διαφορα φαινομενα, πχ στην χιονοπτωση.
Η θερμοκρασια wet-bulb ή αλλιως θερμοκρασια υγρου θερμομετρου ουσιαστικα δινει την θερμοκρασια που θα εχει ενα θερμομετρο υδραργυρου πχ, εαν τυλιξουμε την βαση του εκει που ειναιι ο υδραργυρος με εναν βρεγμενο πανι και επιταχυνουμε την εξατμιση (ωστε να παρουμε σαφεστερη μετρηση) με εναν ανεμιστηρα.
Το θερμομετρο σε αυτη την περιπτωση θα δειχνει μικροτερη θερμοκρασια απο ενα κανονικο θερμομετρο λογω εξατμισης(το νερο σε υγρη μορφη του πανιου εχει μικροτερη κινητικη ενεργεια απο το νερο σε μορφη αεριου(υδρατμος-πχ ο αερας γυρω μας περιεχει υδρατμους-αυτο ειναι που μετραμε αλλωστε με την υγρασια/σχετικη υγρασια κλπ)), οποτε αφου κατα την εξατμιση παιρνουμε περισσοτερους υδρατμους (νερου) αρα παμε απο υγρο νερο σε αεριο νερο, θα εχουμε αυξηση της κινητικης ενεργειας των μοριων του νερου για να συμβει αυτη η αλλαγη φασης. Φυσικα αυτη την ενεργεια την παιρνουν απο το περιβαλλον(απο τον αερα) και αρα η ενεργεια του περιβαλλοντος(αερα) μικραινει οποτε αφου η θερμοκρασια δειχνει απλως το ποση κινητικη ενεργεια εχει ενα σωμα, αρα και η θερμοκρασια του αερα θα μικρυνει.
Η θερμοκρασια υγρου θερμομετρου εχει αμεση σχεση με το αν το χιονι που πεφτει πανω θα επιβιωσει ή οχι πεφτοντας στο εδαφος. Και ειναι αυτη που μας δειχνει καθαρα το αν θα λιωσει το χιονι ή θα παραμεινει υπο μορφη στερεου νερου, δηλαδη χιονιου.
•Αν λοιπον η wet-bulb θερμοκρασια Tw, ειναι μικροτερη ή ιση με μηδεν βαθμους Κελσιου τοτε το χιονι δεν λιωνει.
•Αν ειναι μεγαλυτερη τοτε λιωνει, αν και πολυ συντομα αν συνεχισει να χιονιζει λογω της εξατμισης και εξαχνωσης του χιονιου, το περιβαλλον ψυχεται περισσοτερο, πεφτει η θερμοκρασια του αερα οποτε πεφτει και η Tw, φτανει στους 0 °C οποτε το χιονι "πιανει".
Να και πως παει η πιθανοτητα πειραματικα(και οχι θεωρητικα) να "πιανει" το χιονι σε σχεση με την Tw του αερα χαμηλα(πχ 2 μετρα απο το εδαφος):
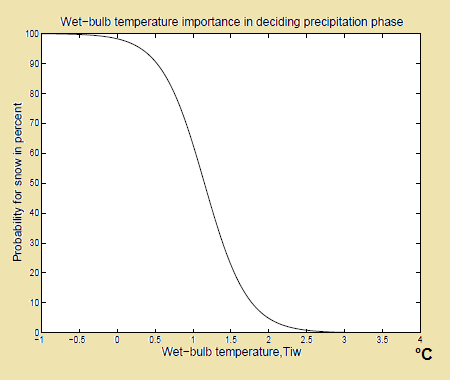
Φαινεται καθαρα οτι η πιθανοτητα για χιονι ειναι σχεδον σιγουρη, 98 % περιπου για θερμοκρασια Tw αερα χαμηλα, ιση με 0 °C.
Απο αυτο φαινεται οτι για να χιονισει αλλά και να το πιασει δεν ειναι αναγκη η θερμοκρασια του αερα να ειναι ανρητικη ή μηδεν βαθμους Κελσιου!
Συνηθως τα διαφορα μοντελα καιρου υπολογιζουν/προβλεπουν την θερμοκρασια στα 2 μετρα πανω απο το εδαφος. Οποτε και οι υπολογισμοι μας βρισκουν την Tw για 2 μετρα απο το εδαφος.
Ομως το χιονι πεφτει στο εδαφος και το εδαφος εχει δικη του θερμοκρασια και ειναι συνηθως (και ανα λογα με την επιφανεια φυσικα) μεγαλυτερη του αερα ψηλοτερα, πχ στα 2 μετρα. Πχ ειδικα οι επιφανειες απο τσιμεντο, πισσα κλπ κρατανε μεσα τους μεγαλα ποσα θερμικης ενεργειας. Οποτε αρχικα ακομη και αν η Tw ειναι 0 °C στα 2 μετρα ή και 10 εκατοστα ακομα πανω απο το εδαφος, υπαρχει ενα στρωμα αερα γυρω απο το εδαφος, περιπου 2 εκατοστων που εχει την θερμοκρασια του εδαφους και ειναι μεγαλυτερη απο το στρωμα αερα πανω απο αυτο, οποτε σε αυτο το στρωμα αερα του εδαφους η Tw θα ειναι μεγαλυτερη των μηδεν βαθμων Κελσιου αρα το χιονι ενω θα πεφει ως χιονι(στερεο) στο εδαφος θα λιωνει. Σιγα σιγα ομως καθως ολο και περισσοτερο χιονι πεφτει, το λιωσιμο και η εξατμιση αυτη του χιονιου(λιωσιμο και μετα εξατμιση) θα κατεβαζει την θερμοκρασια του μικρου αυτου στρωματος αερα κοντα στο εδαφος και θα φτασει καποια στιγμη με Tw = 0 °C οποτε και το χιονι θα πιανει στο εδαφος και δεν θα λιωνει. Βεβαια το εδαφος θα συνεχισει να δινει θερμικη ενεργεια μεσω θερμοτητας στο χιονι που θα εχει πιασει πανω του, αλλά καποια στιγμη θα σταματησει.
Συνηθως τα μοντελα υπολογιζουν την θερμοκρασια στα 2 μετρα πανω απο το εδαφος οποτε για να βρουμε αν θα χιονισει και θα πιασει ή οχι ή εστω να εχουμε μια καλη εκτιμηση αυτου θα πρεπει να βρουμε την wet bulb (Tw) στο εδαφος.
Συνηθως το εδαφος στο τσιμεντο ή στην πισσα σε μια πολη εχει απο 2 εως και 4 βαθμους παραπανω απο τον αερα οποτε αρχικα η θερμοκρασια την οποια λαμβανουμε υποψη για να βρουμε την θερμοκρασια Tw ειναι κατα καποιους βαθμους μεγαλυτερη. Η υγρασια απο την αλλη ειναι περιπου η ιδια οποτε στους υπολογισμους μας λαμβανουμε την υγρασια/σχετικη υγρασια που δινουν τα μοντελα. Τα μοντελα δινουν επισης την θερμοκρασια του dew point(Td)(σημειο δροσου) και μπορουμε και μεσω αυτου να βρουμε την Tw.
Για να βρεθει η Tw μιας ποσοτητας αερα, αρκει να ξερουμε την Τ, θερμοκρασια αυτου καθως και την σχετικη υγρασια RH.
Το ιδιο και για to Td(dew point temperature-σημειο δροσου δηλαδη).
Επισης η Tw, βρισκεται ξεροντας τα Τ και Td.
Συμβολισμοι:
Τ: θερμοκρασια αερα(θερμοκρασια ξηρου θερμομετρου) σε βαθμους Κελσιου
Τd: σημειο δροσου - θερμοκρασια dew point σε βαθμους Κελσιου
Tw: wet bulb - θερμοκρασια υγρου θερμομετρου σε βαθμους Κελσιου
RH: σχετικη υγρασια (πχ 0.72 για 72% σχετικη υγρασια)
P: ατμοσφαιρικη πιεση σε hPa (mbar).
►Αρχικα να δουμε πως υπολογιζεται το Td(σημειο δροσου) εχοντας ως γνωστα τα Τ και RH.
Ισχυει:
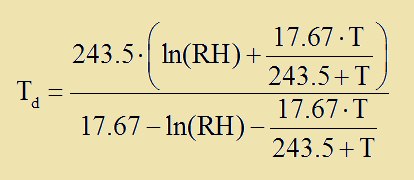
Οπου ln(x) συμβολιζει τον φυσικο λογαριθμο(με βαση το e) του x.
►Υπολογισμος Tw εχοντας ως γνωστα τα Τ και RH και P.
Ισχυει:
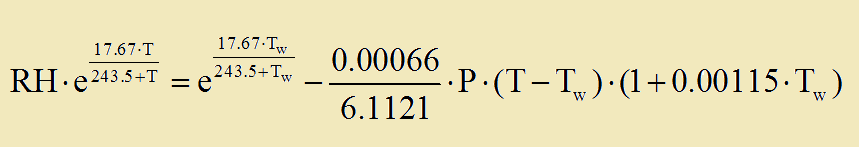
Οπου e ειναι ο αριθμος του Euler (e ~= 2.7 1828 1828 459045....).
H "φοβερη" αυτη εξισωση δεν εχει αναλυτικη λυση αλλά μπορει ευκολα να λυθει με λιγη αριθμητικη αναλυση με την μεθοδο Newton-Raphson πχ ωστε να βρεθει η τιμη της Wet-bulb.
►Υπολογισμος Tw εχοντας ως γνωστα τα Τ και Td και P.
Ισχυει:
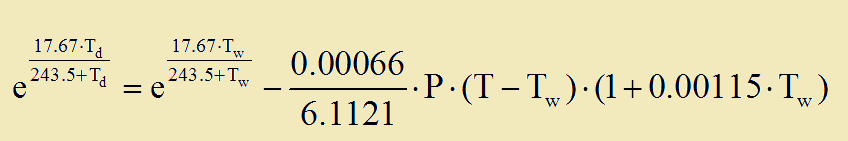
Το ιδιο και εδω με την χρηση της Newton-Raphson.
Δεν υπάρχουν σχόλια:
Δημοσίευση σχολίου